Møller scattering

Feynman diagrams
t-channel
u-channel

Møller scattering is the name given to electron-electron scattering in Quantum Field Theory. The electron interaction that is idealized in Møller scattering forms the theoretical basis of many familiar phenomena such as the repulsion of electrons in the Helium nucleus. While formerly many particle colliders were designed specifically for electron-electron collisions, more recently electron-positron colliders have become more common. Nevertheless Møller scattering remains a paradigmatic process within the theory of particle interactions.

In quantum electrodynamics, there are two tree-level Feynman diagrams describing the process: a t-channel diagram in which the electrons exchange a photon and a similar u-channel diagram. Crossing symmetry, one of the tricks often used to evaluate Feynman diagrams, in this case implies that Møller scattering should have the same cross section as Bhabha scattering (electron-positron scattering).

In the electroweak theory the process is instead described by four tree-level diagrams: the two from QED and an identical pair in which a Z boson is exchanged instead of a photon. The weak force is purely left-handed, but the weak and electromagnetic forces mix into the particles we observe. The photon is symmetric by construction, but the Z boson prefers left-handed particles to right-handed particles. Thus the cross sections for left-handed electrons and right-handed differ. The difference was first noticed by the Russian physicist Yakov Zel'dovich in 1959, but at the time he believed the parity violating asymmetry (a few hundred parts per billion) was too small to be observed. This parity violating asymmetry can be measured by firing a polarized beam of electrons through an unpolarized electron target (liquid hydrogen, for instance), as was done by an experiment at the Stanford Linear Accelerator Center, SLAC-E158.[1] The asymmetry in Møller scattering is

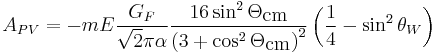A_{PV}=-m E \frac{G_F}{ \sqrt{2} \pi \alpha } \frac {16 \sin^2 \Theta_{\textrm{cm}}} {\left(3%2B\cos^2 \Theta_{\textrm{cm}} \right)^2 } \left( \frac{1}{4} - \sin^2 \theta_W \right) ,

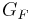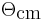where m is the electron mass, E the energy of the incoming electron (in the reference frame of the other electron), G_F is Fermi's constant, \alpha is the fine structure constant, \Theta_{\textrm{cm}} is the scattering angle in the center of mass frame, and 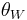\theta_W is the weak mixing angle, also known as the Weinberg angle.

QED computation

References

  1. ^ Younus, I. (October 2004). A. Para. ed. First Results from E158 Measuring Parity Violation in Moller Scattering. American Institute of Physics Conference Series. 721. pp. 367–370. Bibcode 2004AIPC..721..367Y. doi:10.1063/1.1818436. 

External links